Chapter 10 Superposition and Standing Waves
Textbook link: Tipler and Mosca, Section 15.1
10.1 Superposition of harmonic waves
In Section 6.1 we showed that the wave equation (eq. (6.3)) is satisfied by any function in the form \(y = f(x \pm vt)\). We can go further than this, and specify general expressions which can satisfy the wave equation.
Specifically, if we have two functions, \(y_1\) and \(y_2\) (Equation (10.1)), which satisfy the wave equation, then their sum (Equation (10.2), including scaling constants \(C_1\) and \(C_2\)) must also satisfy the wave equation.
\[\begin{equation} \begin{array}{rcl} y_1 &=& A_1 \sin\left[k_1(x \pm vt)\right] \\ y_2 &=& A_2 \sin\left[k_2(x \pm vt)\right] \\ \end{array} \tag{10.1}) \end{equation}\]
\[\begin{equation} y_3 = C_1 y_1 + C_2 y_2 \tag{10.2} \end{equation}\]
Using double angle formulae we can demonstrate that \(y_3\) can also be written in the form \(y = f(x \pm vt)\), thus satisfying the wave equation.14 Therefore, the new wave \(y_3\) is a linear superposition of the original waves \(y_1\) and \(y_2\).
It is worth remembering that the wave equation was derived in the case of small amplitude disturbances; therefore if the vibration amplitudes become too large, the principle of superposition may fail. This can lead to some very interesting effects, including non-linear optics15
10.2 Two waves with same amplitude and frequency
Let’s now consider two waves with the same amplitude and frequency; but differing in phase (Equation (10.3)):
\[\begin{equation} \begin{array}{rcl} y_1 &=& y_0 \sin (kx - \omega t) \\ y_2 &=& y_0 \sin (kx - \omega t +\delta ) \\ \end{array} \tag{10.3} \end{equation}\]
If the two waves are superimposed, for example if they are travelling through the same medium, the resultant wavefunction is just the sum of \(y_1\) and \(y_2\) (Equation (10.4)):
\[\begin{equation} \begin{array}{rcl} y &=& y_1 + y_2 \\ &=& y_0 \sin (kx - \omega t) + y_0 \sin (kx - \omega t +\delta ) \end{array} \tag{10.4} \end{equation}\]
In many situations it is mathematically simpler to use the complex exponential notation to treat waves and oscillations. However, in the case of a linear addition of two waves, it is simpler to just use trigonometric identities.
Here we will use the identity:
\[\begin{equation} \sin\theta_{1}+\sin\theta_{2} = 2\sin\left(\frac{\theta_{1}+\theta_{2}}{2}\right)\cos\left(\frac{\theta_{1}-\theta_{2}}{2}\right) \end{equation}\]
… we obtain:
\[\begin{equation} y = 2y_{0}\sin\left(kx-\omega t + \frac{\delta}{2}\right)\cos\left(\frac{-\delta}{2}\right) \tag{10.5} \end{equation}\]
As an aside, we can do the same thing with complex notation; we can write our wave superposition as follows:
\[\begin{equation} y = y_{1} + y_{2} = y_{0}e^{i(kx - \omega t)} + y_{0}e^{i(kx - \omega t + \delta)} \end{equation}\]
Remembering that we are interested in the ‘imaginary’ component at the end since we started with \(y_1\) and \(y_2\) as sine waves, we can write this superposition as:
\[\begin{equation} y = y_0 e^{i(kx-\omega t)}\left( 1 + \mathrm{e}^{\mathrm{i}\delta} \right) \end{equation}\]
Figure 10.1: We can illustrate addition of complex numbers on an Argand diagram; here we show the sum \(\left( 1 + \mathrm{e}^{\mathrm{i}\delta} \right)\); the result of this is the argument is halved from \(\delta\) to \(\frac{\delta}{2}\).
We can show using an Argand diagram (Figure 10.1) that the term \((1 + \mathrm{e}^{\mathrm{i}\\delta})\) is equal to \(2\cos \left(\frac{\delta}{2}\right)e^{i\frac{\delta}{2}}\), and hence:
\[\begin{equation} y = 2y_0 \cos(\delta/2) e^{i(kx-\omega t + \delta/2)} \end{equation}\]
When we expand this expression using De Moivre’s theorem, we obtain the same result as in Equation (10.5):
\[\begin{equation} y = \underbrace{2 y_0 \cos \left( \frac{\delta}{2} \right)}_{\textsf{New amplitude}} \underbrace{\sin \left( kx - \omega t + \frac{\delta}{2} \right)}_{\textsf{Travelling wave}} \tag{10.6} \end{equation}\]
This tells us that the resulting wave has the same frequency as the component waves, but a different amplitude and phase. This new amplitude is given by the expression in Equation (10.7):
\[\begin{equation} A_{\textsf{new}} = 2 y_0 \cos \left( \frac{\delta}{2} \right) \tag{10.7} \end{equation}\]
There are three special cases to be aware of:
- If \(\delta = 0\), the waves are exactly in phase and the waves add together (constructive interference), with amplitude \(A = 2 y_0\);
- If \(\delta = \pi\), the waves are exactly out of phase and the waves subtract (destructive interference), and the amplitude \(A = 0\);
- If \(\delta = \frac{2\pi}{3}\), the resultant wave has exactly the same amplitude as the input waves.
All three of these cases can be derived by substituting the relevant value of \(\delta\) into Equation (10.7).
10.3 Standing waves
A standing wave is a specific outcome which occurs when a wave is confined to space (for example on a piano string) and it reflects at the boundaries and travels back along its original path. This leads to waves travelling in both directions which combine by superposition. Only certain frequencies can exist in a standing wave, as the superposition leads to a stationary pattern called a standing wave.
10.4 Wave function for a standing wave
In order to fully consier a standing wave, we need to derive the form of its wavefunction. To do this, we consider two waves travelling in opposite directions along a string (Equation (10.8)). Because one is a reflection of the other (they each reflect from the boundaries), they will have the same frequency and phase.
\[\begin{equation} \begin{array}{rcl} y_1 &=& y_0 \sin (kx - \omega t) \\ y_2 &=& y_0 \sin (kx + \omega t) \\ \end{array} \tag{10.8} \end{equation}\]
The resultant vertical displacement of the string is then the sum of these two waves (Equation (10.9)):
\[\begin{equation} \begin{array}{rcl} y &=& y_1 + y_2 \\ y &=& y_0 \sin (kx - \omega t) + y_0 \sin (kx + \omega t) \\ \end{array} \tag{10.9} \end{equation}\]
We can add these directly using a trigonometric identify or we can work in the complex notation:
\[\begin{equation} \begin{array}{rcl} y &=& y_0 \sin (kx - \omega t) + y_0 \sin (kx + \omega t) \\ &=& y_0 \mathrm{e}^{\mathrm{i}(kx - \omega t)} + y_0 \mathrm{e}^{\mathrm{i}(kx + \omega t)} \\ &=& y_0 \mathrm{e}^{\mathrm{i}kx} \left( \mathrm{e}^{-\mathrm{i}\omega t} + \mathrm{e}^{\mathrm{i}\omega t} \right) \end{array} \tag{10.10} \end{equation}\]
We can use either an Argand diagram or De Moivre’s theorem to show that the term \(\left( \mathrm{e}^{-\mathrm{i}\omega t}+ \mathrm{e}^{\mathrm{i}\omega t} \right) = 2 \cos \omega t\), and hence:
\[\begin{equation} y = 2 y_0 \cos \omega t \mathrm{e}^{\mathrm{i}kx} \end{equation}\]
We can now expand the complex exponent using De Moivre’s theorem again and, remembering we are interested in the ‘imaginary’ component (as this contains the desired sine function), and we obtain the result in Equation (10.11):
\[\begin{equation} y = \underbrace{2 y_0 \cos \omega t}_{\textsf{time-dependent amplitude}} \underbrace{\sin kx}_{\textsf{static wave}} \tag{10.11} \end{equation}\]
This result describes a static wave, \(y = \sin kx\) whose amplitude varies in time as \(A = 2 y_0 \cos \omega t\). Note that it is possible to obtain this result via a trigonometric identity also.
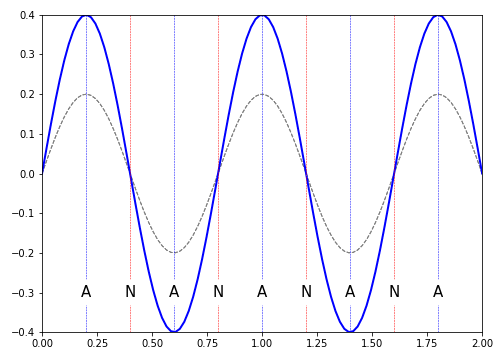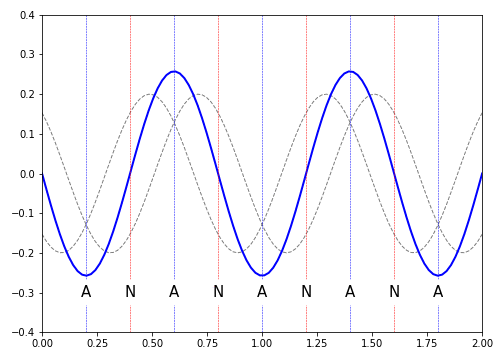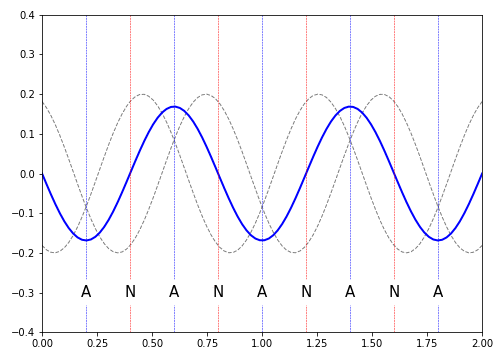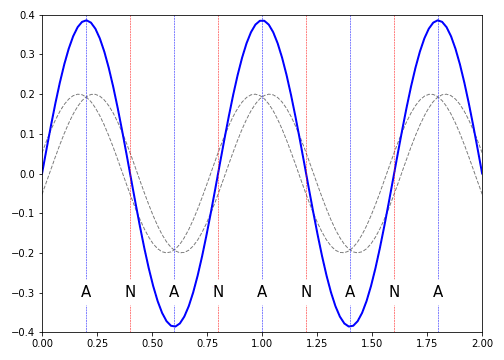
Figure 10.2: A standing wave is the result of two waves equal in frequency and amplitude moving past each other. This forms a static wave whose amplitude varies in time, and has nodes (N) and antinodes (A) present in the waveform. Here we show the fifth harmonic; 5 antinodes and a wavelength \(\lambda = 2/5 = 0.8\).
This standing wave is illustrated in Figure 10.2; but we notice that there are boundary conditions enforced; namely that the ends of the string are fixed at a constant, zero displacement; i.e.:
- \(y = 0\) at \(x = 0\), and:
- \(y = 0\) at \(x = L\) at all times \(t\)
…where \(L\) is the length of the string. From this we deduce that \(\sin kL = 0\) and therefore there are a family of solutions for \(k\) and \(\lambda\), known as harmonics.
- If \(\sin kL = 0\), then \(kL = 0, \pi, 2\pi, \dots\), or \(k_n L = n\pi\)
- Additionally, \(\lambda_n = \frac{2\pi}{k_n} = \frac{2L}{n}\) where \(n = 1, 2, 3, \dots\)
In other words, the vibrational modes are **quantised* due to the boundary conditions.
10.5 Waves on strings fixed at both ends
We have described the mathematics of standing waves; let’s now apply this to a wave travelling on a string which is fixed at both ends. Figure 10.3 illustrates the fundamental wavelength of the string, which corresponds to twice the length of the string.
Figure 10.3: The fundamental frequency, or first harmonic. This is one half-wavelength enclosed in the boundaries and has a single antinode.
We can then visualise the harmonics within the standing wave on this fixed string (Figure 10.4)
Figure 10.4: The second, third, fourth and fifth harmonics of a standing wave on a string. Notice that the \(n\)th harmonic has \(\frac{n}{2}\) wavelengths contained in the space.
The modes of vibration (resonances) shown in Figure 10.4 illustrate the occurence of nodes (points which do not move) and antinodes (points with the maximum vibration amplitudes). Note also that the end-points of the string must be nodes as well, as these points are fixed.
In general, the \(n\)th harmonic will have \(\frac{1}{n} \times\) wavelength and \(n \times\) the frequency of the fundamental vibration shown in Figure 10.3.
| Harmonic | \(\lambda\) | \(f\) |
|---|---|---|
| Fundamental, first | \(2L\) | \(f_1\) |
| Second | \(L\) | \(2f_1\) |
| Third | \(\frac{2L}{3}\) | \(3f_1\) |
| Fourth | \(\frac{L}{2}\) | \(4f_1\) |
| Fifth | \(\frac{2L}{5}\) | \(5f_1\) |
| \(n\)th | \(\frac{2L}{n}\) | \(nf_1\) |
In general, for the \(n\)th harmonic:
- Wavelength is given by \(\lambda_n = \frac{2L}{n}\)
- Frequency is given by \(f = nf_1 = \frac{nv}{\lambda_1} = \frac{nv}{2L}\)
…where \(v\) is the phase velocity (the speed of propagation of the wave along the string).
The resonant frequencies, or harmonics, of the string are known as its natural frequencies. Any string will resonate with maximum amplitude when excited with these frequencies, and this set of harmonics are known as a harmonic series. The actual harmonics heard when the string is excited will depend on the manner of its excitation; e.g. a string plucied at its centre will only display the odd harmonics; i.e. those with an anti-node in the centre.
In stringed instruments (violin, piano, guitar etc.) the vibration of the string is amplified by a mechanical resonator; a soundboard in the case of the piano, or resonant cavities for a guitar or violin. These resonators must be carefully designed to resonate equally well over a wide range of frequencies.
10.6 Organ pipes and other wind instruments
In contrast to a vibrating string, wind instruments rely on a resonance within a column of air. We can model these pipes as a simple pipe, resonating at its natural frequencies when air is blown into (or across) an opening at one end. The resonant behaviour will differ depending on whether the other end of the pipe is open or closed. We will consider each of these cases in turn.
10.6.1 Pipes open at both ends
In this model, the column of air is able to vibrate at its ends, so we have a similar set of harmonics as for a string, but with displacement antinodes at its ends (the air can vibrate freely at the ends of the tube). There is a second set of nodes/antinodes corresponding to the pressure; these do not align with the displacement nodes/antinodes; rather a pressure node aligns with a displacement antinode and vice versa. (if an air molecule does not move, we have a displacement node, but it is continuously ‘squashed’ from both sides by the oscillating air molecules, so experiences the biggest pressure change).
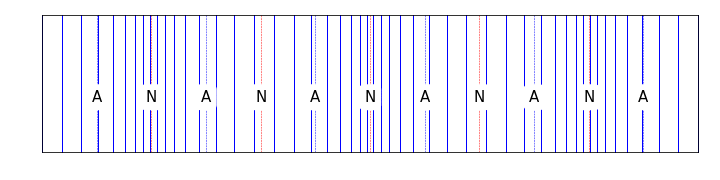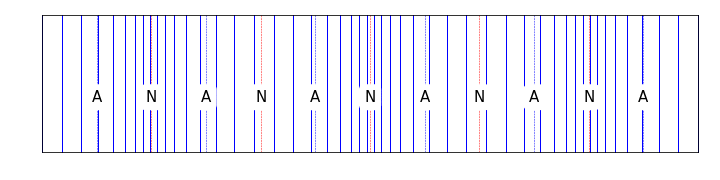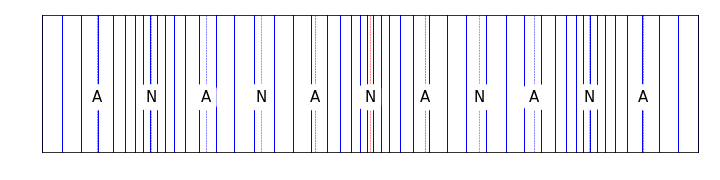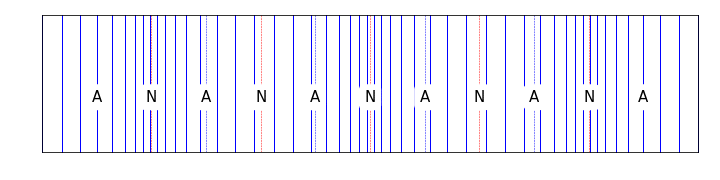
Figure 10.5: This image shows the node/antinode structure of a standing wave in a closed tube. Note the presence of a displacement node at either end where molecules are compressed against the end of the tube
We observe all harmonics in this system; there are no concerns about ‘position of plucking’ that there is for the string. The displacement of the air molecules extends a little beyond the ends of the tube, so the effective length is given by \(L_\textsf{eff} = L + \Delta L\), where \(\Delta L\) is a small end correction. Therefore:
\[\begin{equation} \lambda_n = \frac{2L_\textsf{eff}}{n} \quad \textsf{and} \quad f_n = \frac{nv}{2L_\textsf{eff}} \end{equation}\]
10.7 Pipe closed at one end
We now have a different situation with different boundary conditions:
- There must be a displacement node at the closed end
- There must be a displacement antinode at the open end
This now gives us a fundamental wavelength four times longer than the effective length of the tube (the shortest node-antinode separation is a quarter wavelength).
This means that we only observe the odd harmonics (the even harmonics would not allow the boundary conditions for this tube).
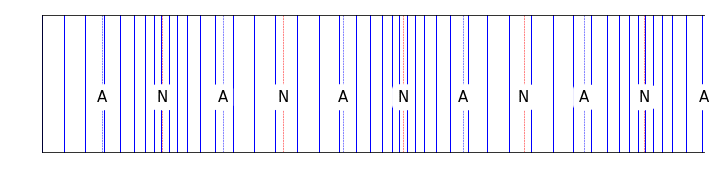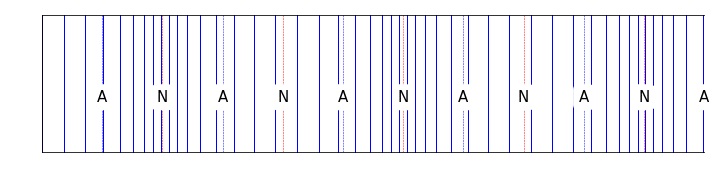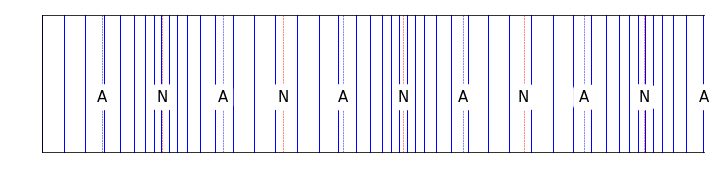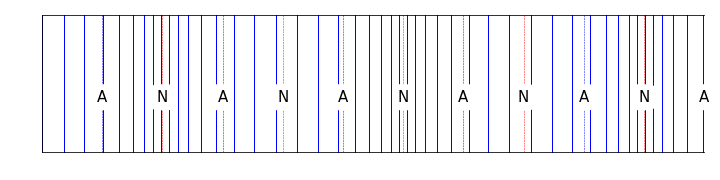
Figure 10.6: For a tube open at one end, the standing waves now have a node at the closed end, and an antinode at the open end. This changes the available harmonics within the tube.
\[\begin{equation} \lambda_n = \frac{4 L_\textsf{eff}}{n} \quad n = 1,3,5,\dots \end{equation}\]
\[\begin{equation} f_n = \frac{nv}{4 L_\textsf{eff}} \quad n = 1,3,5,\dots \end{equation}\]